Investigadores utilizan técnicas de lógica computacional para detectar sesgos en el aprendizaje

¿Qué relaciona a la lógica con las ciencias cognitivas? En este proyecto, científicos del ICC recurren a la lógica proposicional para estudiar cómo influyen los sesgos en el aprendizaje de nuevos conceptos o categorías, especialmente cuando cada uno de esos conceptos es descripto con fórmulas distintas o adquiere diferentes posibilidades de simbolizarse. El trabajo es realizado por investigadores del Grupo en Lógica y Computabilidad y parte de entender la Teoría algorítmica de la información.

Dentro de las Ciencias de la Computación, un área poco explorada en la divulgación científica es la Lógica y Computabilidad. Si bien se trata de un área de base teórica, resulta clave para entender los fundamentos en los que se estructura un lenguaje o un sistema formal de representación. En particular, investigadores del ICC realizan un valioso trabajo de formalización utilizando, entre otras herramientas, la lógica proposicional para problemas de ciencias cognitivas.

¿De qué hablamos cuando hablamos de lógica proposicional? A veces entendida como “lógica de orden cero”, es un sistema formal cuyos elementos más simples representan proposiciones, y que posee operadores lógicos que se aplica sobre proposiciones para formar otras de mayor complejidad (por ejemplo, el ∧ es un operador binario, y el ¬ es uno unario). Cualquier sistema lógico basado en la lógica proposicional es decidible y en un número finito de pasos se puede determinar la verdad o falsedad semántica de una proposición. Esto hace que la lógica proposicional sea completa y con una semántica sencilla de expresar.

“La pregunta principal que nos hacemos tiene que ver con la cognición humana, sobre qué es el aprendizaje y cómo aprendemos. Esta pregunta nos la hacemos teniendo en cuenta que las ciencias cognitivas son multidisciplinarias, no sólo involucran a la computación sino también a la neurobiología, psicología, redes neuronales e inteligencia artificial”, precisa Sergio Abriola, investigador del ICC e integrante del Grupo en Lógica y Computabilidad (GLyC).  

Sergio Abriola

El investigador puntualiza que el grupo parte de una noción de aprendizaje que se relaciona con la compresión de datos. Dicho de otro modo, a partir de cierta cantidad de datos presentados se busca formar un concepto y ese concepto se debe describir de la forma más breve posible. “Uno busca regularidades en los datos y en base a esto da una descripción breve pero precisa que explique el ‘concepto’ que los datos determinan. Usando el principio de longitud mínima de descripción, que formuló Peter Grünwald, tenemos una herramienta para estudiar aprendizaje de conceptos desde una perspectiva de complejidad. Este paradigma es libre de modelos en el sentido de que las descripciones tienen una interpretación clara más allá de cómo se generalizan a datos no observados”, explica Abriola, quien además es Doctor en Ciencias Matemáticas de la UBA. 

Este trabajo apunta a poder formalizar esos nuevos conceptos en un lenguaje de símbolos u operadores específicos. La investigación se vale de la famosa Complejidad de Kolmogorov (muy usada en teoría algorítmica de programas). Para expresarlo de manera sencilla: la complejidad de una cadena de letras y dígitos es la longitud de la más corta posible descripción de la cadena en algún lenguaje de descripción universal fijo y se puede definir para cualquier objeto matemático que uno quiere usar para expresar conceptos. El problema se complejiza aún más cuando se introduce el contexto de una situación de aprendizaje, por ejemplo, cuando a una persona se le presentan diferentes conceptos para aprenderlos, los resultados obtenidos pueden ser distintos de acuerdo a la percepción, atención selectiva o experiencia previa del sujeto de aprendizaje, más allá de la representación racional de los conceptos.

Sesgos clásicos en el aprendizaje

El concepto de sesgo cognitivo fue introducido en economía por Daniel Kahneman y Amos Tversky en 1972, a raíz de una investigación sobre cómo procesa nuestra mente las probabilidades y descripciones muestrales, en lo que se conoce como la Ley de los pequeños números. Los investigadores llegaron a la conclusión de que existen influencias emocionales y patrones de pensamiento que hacen que no seamos capaces de interpretar adecuadamente (racionalmente) la información que recibimos. Un ejemplo de ello es el sesgo de anclaje, en el que se le da mayor peso a la primera información que se nos provee y que en un planteo matemático podría hacer que nuestro resultado estimado se acerque más al número que se nos mencionó en la consigna del problema. E incluso el sesgo de confirmación, que tiene la tendencia a favorecer, buscar, interpretar, y recordar, la información que confirma las propias creencias o hipótesis, dando desproporcionadamente menos consideración a posibles alternativas.

Puntualmente, el proyecto de los investigadores aborda algunos de estos sesgos. Tal es así que consiste en crear dos fórmulas de lógica proposicional que son mínimas (lo que significa que no se pueden reducir a una fórmula equivalente más pequeña) y que representan dos conceptos distintos sobre el universo completo (ver Figura 1). No obstante, cuando el universo a ser mostrado es seleccionado de cierta manera, ambas fórmulas tienen el mismo poder explicativo, aunque se generalizan de distinta manera al universo completo.  En este contexto, se trabaja con el sesgo de atención selectiva donde el historial del sujeto le inclina a una preferencia por considerar ciertos operadores o variables proposicionales por encima del resto. 

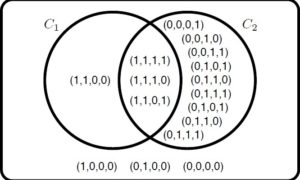
Figura 1: Un universo proposicional de cuatro variables, y dos conceptos C_1 y C_2 que corresponden a las fórmulas (p_1∧ p_2) y (p_3 ∨ p_4) respectivamente.

“Uno de los sesgos que estamos estudiando es qué tipo de influencia tiene la experiencia pasada a la hora de encontrar fórmulas sucintas que expliquen un concepto. Si por ejemplo uno anteriormente utilizó la variable proposicional correspondiente con un triángulo o círculo en una descripción de un concepto, posiblemente vaya a prestarle atención preferencial a esa variable luego”, subraya Abriola (ver figuras 2 y 3). Otro de los temas en que los investigadores se detienen, dentro del área de la lógica proposicional, es la detección particular de ciertos operadores para representar un concepto. “Un ejemplo claro es el uso del O e Y (disyunción y conjunción), ya que cómo funcionan estos operadores puede depender de cuestiones de atención e incluso de experiencia previa. Existen estudios conductuales realizados en niños donde se ve que a partir de cierta edad se aprende el O pero el Y resulta más natural. Lo que también vemos en general en nuestros estudios es que hay un sesgo preferencial hacia la conjunción, que se puede entender como una diferencia en los pesos relativos entre ambos operadores lógicos.”, complementa el investigador del ICC.

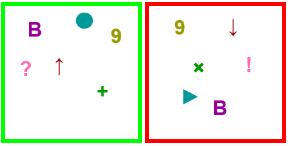
Figura 2: Representaciones visuales de dos elementos en un universo proposicional de 6 variables. Cada color corresponde a una variable proposicional, y el símbolo concreto indica su valor.

Figura 3: Un universo parcial en el cual ejemplos positivos de un concepto están marcados en verde, y los negativos en rojo. Aquí el concepto presentado podría verbalizarse como “Las cajas que contienen simultáneamente una flecha para arriba y un signo de interrogación”, o alternativamente como “Cajas conteniendo un círculo o un signo más(+)”

Abriola plantea que un error de razonamiento lógico que muchas veces puede encontrarse es el de error converso (confusión de necesidad y suficiencia), que a partir de “A entonces B” y “B” concluye “A”. Un ejemplo ilustrativo de esta falacia es, sabiendo que una enfermedad siempre viene acompañada por ciertos síntomas que uno está experimentando, concluir que se tiene esta enfermedad. Otra falacia (esta vez probabilística) que puede aparecer en el ejemplo análogo es la negligencia de la frecuencia base; esto es, por más que la “enfermedad A” conlleve casi siempre los “síntomas B”, no considerar que existen otros fenómenos (quizás mucho más frecuentes) que también pueden provocar (con cierta probabilidad, quizás baja) los mismos “síntomas B”.

En el ámbito científico algunos de los sesgos de selección consisten (valga la redundancia) en tomar datos sesgados cuya muestra o población no representa aleatoriamente al universo considerado, o el mal uso del análisis de datos para representar patrones en los datos que pueden presentarse como estadísticamente significativos, lo cual aumenta drástica y ocultamente el riesgo de falsos positivos (conocido en la jerga como “p-hacking”), o el sesgo de publicación (propensión a publicar trabajos científicos que tienen resultados novedosos y no aquellos trabajos que no encontraron efectos estadísticamente significativos). 

Claro que las posibilidades que abre el uso de técnicas de lógica computacional para estudiar la cognición humana no se agotan allí y el desafío a futuro de los investigadores del ICC es seguir profundizando en estos trabajos recientes para ir mucho más allá, inclusive en temas de neurobiología: entender por ejemplo patrones de activación neuronales ante diversas tareas cognitivas, casos de percepción multiestable, pensamiento automático versus pensamiento deliberado, aprendizaje y reconocimiento de conceptos, etc.  

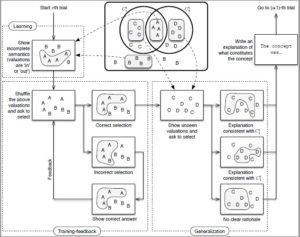
Figura 4: Esquema del diseño experimental que están realizando los investigadores.

Algunas aplicaciones de la lógica y computabilidad a dominios de la ciencia

De acuerdo a la explicación de Sergio Abriola, un eje de estas investigaciones es la denominada hipótesis del Lenguaje del pensamiento, que propone un lenguaje mental sobre el cual ocurre la cognición, muchas veces asumiendo una estructura lógica para estas expresiones. En general, los estudios sobre sobre el funcionamiento de la cognición humana se podrían aplicar a problemas de inteligencia artificial, aprendizaje no supervisado, redes neuronales y estudios de neurobiología, detección de imágenes y procesamiento del lenguaje, entre muchos otros dominios