Authors: Flavia Bonomo-Braberman, Eric Brandwein, Fabiano S. Oliveira, Moysés S. Sampaio Jr., Agustin Sansone and Jayme L. Szwarcfiter.
Abstract:
Interval graphs and proper interval graphs are well known graph classes, for which several generalizations have been proposed in the literature. In this work, we study the (proper) thinness, and several variations, for the classes of cographs, crowns graphs and grid graphs.
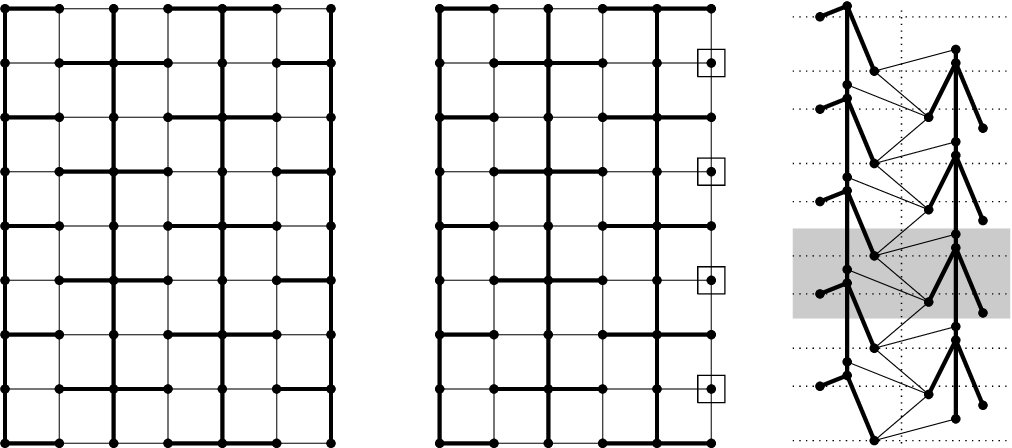
We provide the exact values for several variants of thinness (proper, independent, complete, precedence, and combinations of them) for the crown graphs CRn. For cographs, we prove that the precedence thinness can be determined in polynomial time. We also improve known bounds for the thinness of n×n grids GRn and m×n grids GRm,n, proving that ⌈n−13⌉≤thin(GRn)≤⌈n+12⌉. Regarding the precedence thinness, we prove that prec-thin(GRn,2)=⌈n+12⌉ and that ⌈n−13⌉⌈n−12⌉+1≤prec-thin(GRn)≤⌈n−12⌉2+1. As applications, we show that the k-coloring problem is NP-complete for precedence 2-thin graphs and for proper 2-thin graphs, when k is part of the input. On the positive side, it is polynomially solvable for precedence proper 2-thin graphs, given the order and partition.
More information: https://arxiv.org/abs/2303.06070