Authors: Flavia Bonomo-Braberman, Julliano R. Nascimento, Fabiano S. Oliveira, Uéverton S. Souza, Jayme L. Szwarcfiter.
Abstract:
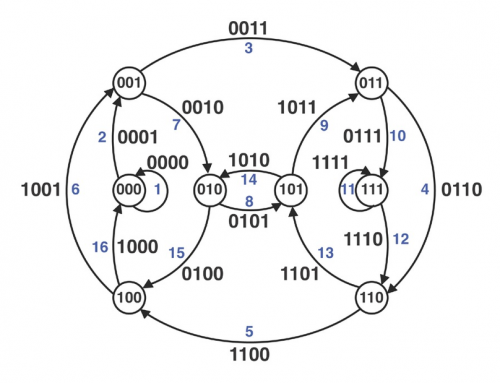
Since many NP-complete graph problems have been shown polynomial-time solvable when restricted to claw-free graphs, we study the problem of determining the distance of a given graph to a claw-free graph, considering vertex elimination as measure. CLAW-FREE VERTEX DELETION (CFVD) consists of determining the minimum number of vertices to be removed from a graph such that the resulting graph is claw-free. Although CFVD is NP-complete in general and recognizing claw-free graphs is still a challenge, where the current best algorithm for a graph G has the same running time of the best algorithm for matrix multiplication, we present linear-time algorithms for CFVD on weighted block graphs and weighted graphs with bounded treewidth. Furthermore, we show that this problem can be solved in linear time by a simpler algorithm on forests, and we determine the exact values for full k-ary trees. On the other hand, we show that CLAW-FREE VERTEX DELETION is NP-complete even when the input graph is a split graph. We also show that the problem is hard to approximate within any constant factor better than 2, assuming the Unique Games Conjecture.
More information:
https://arxiv.org/abs/2004.05672