Intersection models and forbidden pattern characterizations for 2-thin and proper 2-thin graphs

Authors: Flavia Bonomo-Braberman and Gastón Abel Brito.

Abstract:
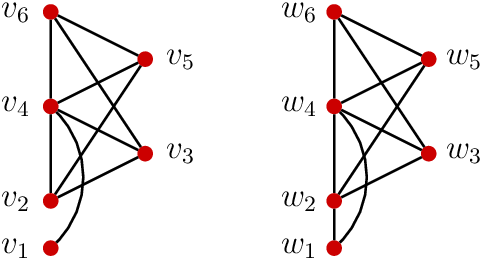
The thinness of a graph is a width parameter that generalizes some properties of interval graphs, which are exactly the graphs of thinness one. Graphs with thinness at most two include, for example, bipartite convex graphs. Many NP-complete problems can be solved in polynomial time for graphs with bounded thinness, given a suitable representation of the graph. Proper thinness is defined analogously, generalizing proper interval graphs, and a larger family of NP-complete problems are known to be polynomially solvable for graphs with bounded proper thinness.

The complexity of recognizing 2-thin and proper 2-thin graphs is still open. In this work, we present characterizations of 2-thin and proper 2-thin graphs as intersection graphs of rectangles in the plane, as vertex intersection graphs of paths on a grid (VPG graphs), and by forbidden ordered patterns. We also prove that independent 2-thin graphs are exactly the interval bigraphs, and that proper independent 2-thin graphs are exactly the bipartite permutation graphs.

Finally, we take a step towards placing the thinness and its variations in the landscape of width parameters, by upper bounding the proper thinness in terms of the bandwidth.

More Information:
https://www.sciencedirect.com/science/article/abs/pii/S0166218X23002354