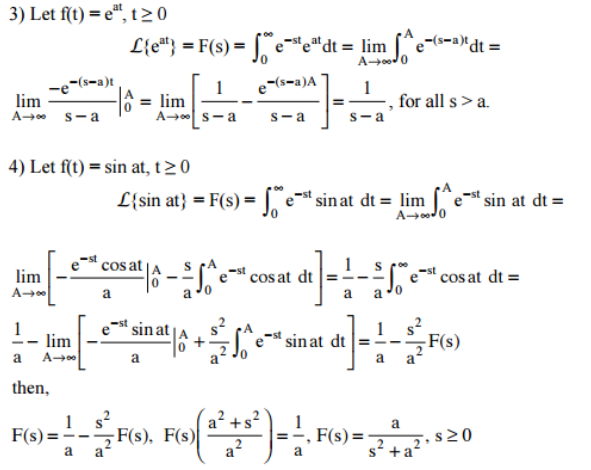Authors: Verónica Becher, Eda Cesaratto.
Abstract:
We show that, in an alphabet of n symbols, the number of words of length n whose number of different symbols is away from (1 – 1/e)n, which is the value expected by the Poisson distribution, has exponential decay in n. We use Laplace’s method for sums and known bounds of Stirling numbers of the second kind. We express our result in terms of inequalities.
More information:
https://www-2.dc.uba.ar/staff/becher/papers/restrictions.pdf